Do We Trust Feature Importance Scores from Random Forests and XGBoost? - NBD Lite #21
Consideration when using the feature importance score.
If you are interested in more audio explanations, you can listen to the article in the AI-Generated Podcast by NotebookLM!👇👇👇
A feature importance score exists when you use ensemble tree-based models such as Random Forest and XGBoost.
rf_model.feature_importances_I have seen many using the score for feature selection and explainability, which is fine.
However, we need to know the caveat on using these scores.
So, this article will focus on what you should consider before using the tree-based feature importance score.
Let’s get into it!
How Does Tree-Based Feature Importance Work?
Before we go in-depth on the caveat, we should understand what the score represents.
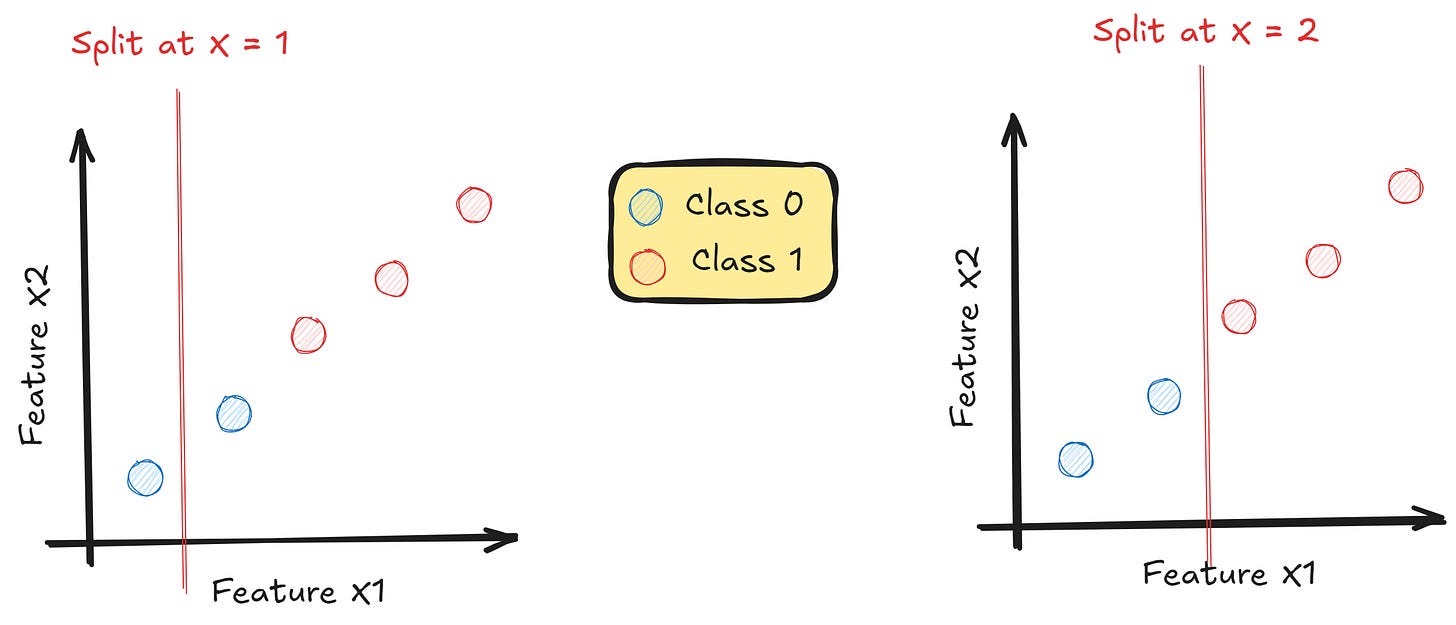
Let’s consider the following dataset example visualization.
We have five samples in a 2-dimension scatter plot with two classes.
In a tree-based model, many methods exist to decide the splitting criteria and the feature importance score based on the technique.
One of the most popular is the Gini Impurity.
Using the sample data above, we can calculate the Gini Impurity score as follows:
We have the Gini Impurity score of 0.52.
Let’s see how we can decide the splitting point with Gini impurity.
For example, the tree-based model would check whether the split at X = 1 is much better than X = 2 or vice versa.
When we say “better,” it means which split provides the better purity. Using the Gini Impurity calculation, we calculate for each split.
We get their Gini Impurity score for each split at the left and right positions. Then, we try to get the weighted Gini Impurity for the split.
If we apply it to the calculation above, it would look like this:
The best split is the one that has the highest purity, which means we want the lowest Weighted Gini. The example above shows that the split at X = 2 is the best.
Now, we will try to understand how the Feature Importance with the Gini Impurity score works.
We would calculate the reduction in Gini impurity for each feature from splitting on certain features.
We calculate the difference between each feature's Gini Parent and the split-weighted Gini.
The sample above shows that the reduction in Gini Impurity is 0.52. That is the feature importance score.
If the feature is used multiple times for splitting, we will use the sum of reduction in Gini impurity.
The feature importance score is the sum of the reduction in Gini impurity or how much the feature contributes to the splitting decision.
Can we trust the tree-based Feature Importance Score?
We can trust the score if we consider them from the method standpoint.
However, as we already established above, the tree-based feature importance score is based on the sum of the reduction in Gini impurity.
It means anything that affects the Gini impurity score would affect the score.
With that in mind, there is going to be some caveat:
1. Bias Towards High-Cardinality Features
Random Forests and XGBoost would inflate the feature importance score to the high-cardinal features.
For example, a numerical feature with many unique values may seem more important because it can be split more often.
This does not necessarily mean the feature has more predictive power; it provides more opportunities for the model to split the data.
It means that the sum of the reduction in Gini impurity would rise with each splitting occurrence.
2. Correlation Between Features Affecting Score
When two or more features are correlated, their feature importance score can be shared.
When information overlaps, the model may use only one for splitting, leading to lower importance scores for the other.
As a result, the feature importance scores for each of the correlated features may be lower than they would be if one of the features were removed.
3. Dependence on Model Hyperparameters
Feature importance scores depend on the hyperparameters.
For example, changing the number of trees or the maximum depth in Random Forests or XGBoost can lead to different importance rankings for features as it would affect the sum of reduction in Gini impurity.
Reducing the number of trees in a Random Forest might cause less reliable features to be selected more frequently, altering the feature importance score.
It is like that we can manipulate the feature importance score with the model hyperparameters.
Conclusion
So, can we trust the feature importance score from the tree-based model? You can trust them if you understand the method used to calculate the feature importance score and the caveat.
That’s all for today! I hope this helps you understand how the feature importance score in the tree-based model works and whether you can trust them.
Are there any more things you would love to discuss? Let’s talk about it together!
👇👇👇