Partial Dependence Plots (PDPs) to Interpret Complex Models - NBD Lite #38

Powerful tool that you might miss previously

Machine Learning projects are only useful if there is trust between the stakeholders and the technical teams.

We can have the most accurate model in the world, but it would be useless if it weren’t used.

In my experience, the best way to build initial trust is to have a machine-learning model that the business can understand.

This is where the explainability concept could help our work.

In today’s article, we will discuss one of the tools for explainability: the Partial Dependence Plots.

What is this tool? Let’s get into it.

---

Partial Dependence Plot

Partial Dependency Plots (PDPs) are visualization tools for machine learning interpretability.

It visualizes the relationship between our model input features and the output predictions of a machine learning model.

The tool is helpful to understand complex and non-linear models, such as ensemble models or neural networks.

How Does PDP Work?

PDPs work by illustrating how the model's predictions change as one or more input values change.

For example, if you have a feature like "average income", PDP can show how changing the income level influences the predicted house price while keeping other factors constant.

To generate a PDP, we would follow the following standard:

• Choose the feature(s) of interest (e.g., "age").

• For each unique value or range of the chosen feature:

  • Fix the value of the feature.

  • Compute the model predictions while varying other features in the training data.

  • Take the average of these predictions for each feature's fixed value.

• Plot the averaged predictions against the fixed feature values.

Python Implementation

Let’s try it out with the Python code example.

We would use the pdpbox package, so we need to install them.

pip install pdpbox

Next, we would train a simple classifier model using the example titanic dataset.

import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from pdpbox import pdp
import seaborn as sns
import matplotlib.pyplot as plt

data = sns.load_dataset('titanic')
data = data.dropna()

X = data[['pclass', 'age', 'sibsp', 'fare', 'adult_male']]
y = data['survived']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = RandomForestClassifier()
model.fit(X_train, y_train)

With the model ready, we would use PDP to interpret the relationship between the feature and the model prediction.

1D PDP

First, we would try to generate a PDP analysis on a single feature, which we called 1D PDP.

feature = 'age'  # Feature to analyze
pdp_iso = pdp.PDPIsolate(
    model=model,
    df=X_train,
    model_features=X_train.columns,
    feature=feature,
    feature_name=feature,
    n_classes=2
)

fig, axes = pdp_iso.plot(plot_lines=True, frac_to_plot=0.1, plot_pts_dist=True)
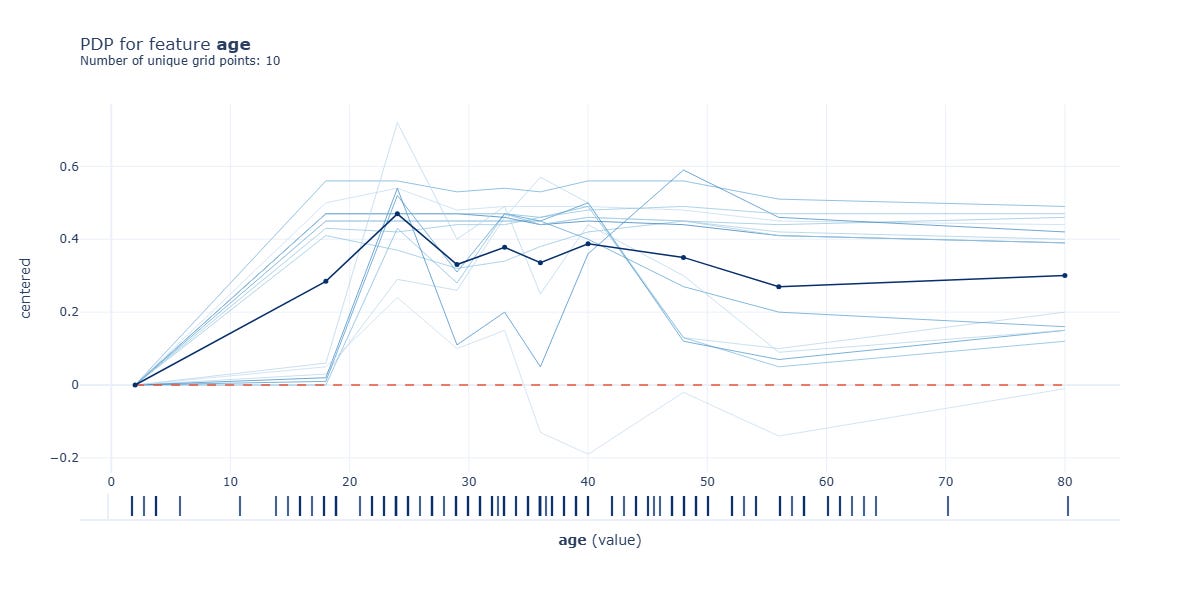
fig

Above is the PDP for the feature “age” with the prediction output from our model. How do we interpret the plot above?

There are a few components you need to understand from the above PDP:

• The main line in bold represents the average effect of the “age” feature on the model's output. If the line is above 0, “age” that range positively contributes to the prediction; if it’s below 0, it has a negative contribution.

• The lighter line shows the individual conditional expectation (ICE) curves for a subset of the data points. It’s useful to provide insight into the variability of the model's behaviour at different “age” values. Basically, the spread and pattern of the line indicate how consistent the effect of the feature “age” is across various data points.

• The dashed red line is the baseline that represents the average prediction across all observations.

The PDP above indicates that the “age” feature has a complex, non-linear effect on the model's predictions.

The main line starts at 0 and rises sharply between ages 10–20, showing a positive contribution, but dips and fluctuates after 20, suggesting mixed or variable effects at higher age values.

The lighter ICE lines highlight significant variability, with some trending upward and others downward, indicating that the impact “age” varies across different data points, potentially due to interactions with other features or subpopulations.

This variability suggests that while “age” consistently contributes positively at lower values, its effect diminishes or stabilizes at higher levels, confirming a non-uniform relationship across the dataset.

That’s how you interpret the PDP for a single feature, but it’s possible to perform PDP analysis for two different features to see how the features interact with the model output.

2D PDP

For feature interaction between two features, we would call them 2D PDP.

We can use the following code in Python to perform the 2D PDP.

features = ['pclass', 'age']
pdp_interact = pdp.PDPInteract(
    model=model,
    df=X_train,
    model_features=X_train.columns,
    features=features,
    feature_names=features,
    n_classes=2  
)

The 2D PDP in the above plot is between the feature “age” and “pclass”. How do we interpret them?

There are a few components we need to understand from the plot above, which include:

• The plot is divided into regions with contour lines representing different prediction probability levels.

• The colour scale on the right shows the range of prediction probabilities, where darker colours (e.g., dark blue) represent higher probabilities, and lighter colours (e.g., light blue) represent lower probabilities.

The plot shows how the predicted probability of the positive class varies depending on the values of “age” and “class” features.

For example, dark blue regions indicate a higher predicted probability (around 0.8), meaning that combinations of “age” and “class” features in these areas are more likely to result in a positive prediction.

Combining both features allows us to use PDP to see which region provides the highest and lowest prediction probability.

Advantages and Disadvantages of PDP

PDP is useful for our data scientist work for many reasons, including:

• Interpretability: PDPs provide a visual way to understand how features impact the model's output.

• Non-Invasiveness: They do not require changes to the model's training process.

However, PDP has some limitations that we can’t ignore:

• Averaging Issue: PDPs show an average effect, which can mask feature interactions if the model’s behaviour varies significantly depending on the values of other features.

• Assumption of Independence: PDPs assume that the plotted feature is not correlated with other features, which might not be true in real-life data.

• Computational Cost: Generating PDPs can be computationally intensive, especially for large datasets or complex models.

As PDP has some limitations, it’s great to use it alongside other interpretability tools, such as LIME or SHAP, to support the result.

---

That’s all you need to know about PDP.

Are there any more things you would love to discuss? Let’s talk about it together!

👇👇👇