Statistik Dasar untuk Data Scientist — Part 2: Probability Distribution
Jika kalian belum membaca bagian pertama series ini, silakan kunjungi link ini untuk membacanya, sebab dasar dari apa yang saya bahas di…
Jika kalian belum membaca bagian pertama series ini, silakan kunjungi link ini untuk membacanya, sebab dasar dari apa yang saya bahas di artikel ini akan merujuk kepada dasar-dasar statistik yang ada di artikel tersebut.
Pada artikel ini saya akan mencoba menjelaskan konsep dari Probability Distribution. Konsep ini penting untuk dipahami oleh seseorang yang ingin ataupun telah menjadi seorang Data Scientist karena Probability Distribution mampu membantu seorang Data Scientist untuk mengenali pola dari suatu variabel acak.
Probability Distribution
Konsep dasar
Mungkin kalian sering melihat gambar diatas, tetapi tidak memahami apa sebenarnya fungsi dari gambar tersebut. Sebenarnya yang saya tunjukkan diatas adalah contoh dari probability distribution, atau lebih tepatnya adalah Normal (Gaussian) Distribution.
Probability Distribution adalah suatu fungsi matematika yang memberikan kemungkinan (likelihood) dari variabel acak untuk memiliki suatu nilai. Dengan kata lain, kemungkinan suatu variabel acak untuk memiliki suatu nilai akan tergantung dari Probability Distribution.
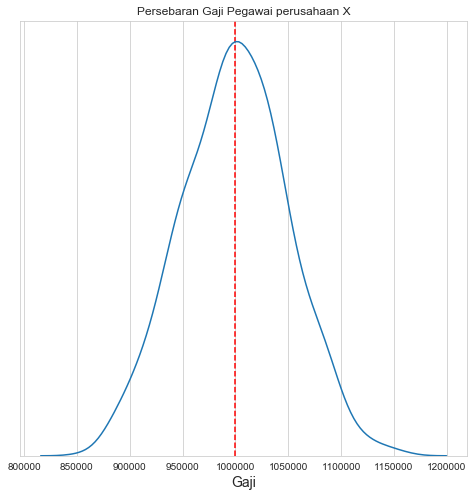
Probability Distribution berguna untuk mengetahui kejadian apa yang paling mungkin terjadi, kemungkinan setiap kejadian yang akan terjadi, dan persebaran terjadinya suatu kejadian. Sebagai contoh, perusahaan X memilki 1000 pegawai dan saya mengambil gaji setiap pegawai yang ada. Jika saya membuat plot distribusi dari gaji pegawai perusahaan X maka dapat digambarkan sebagai berikut.
Distribusi data diatas memberikan kita suatu Probability Distribution yang memberikan gambaran persebaran kemungkinan gaji di perusahaan X. Kita dapat mengetahui bahwa jika kita mengambil nilai gaji secara acak dari pegawai perusahaan X maka kemungkinan besar kita akan mendapatkan nilai yang mendekati garis merah atau mean dari gaji. Kebalikannya, kemungkinan kita secara acak mendapatkan pegawai dengan gaji kurang dari 900000 atau lebih dari 1100000 adalah kecil.
Sifat
Di dalam statistik, probability biasa dituliskan sebagai berikut.
p(x) = kemungkinan suatu variabel acak memiliki nilai x
Jika dijumlahkan, seluruh kemungkinan yang mungkin terjadi di dalam probabilty distribution akan berjumlah sama dengan 1. Terlebih lagi kemungkinan ini hanya boleh diantara nilai 0 hingga 1 saja.
Selain itu, tergantung dari tipe variabel yang kita miliki, tipe dari Probability Distribution ini sendiri akan berbeda, yaitu:
Discrete Probability Distribution atau Probability Mass Function untuk variabel discrete atau categorical
Continuous Probability Distribution atau Probability Density Function untuk variabel continuous atau kuantitatif
Probability Mass Function (PMF)
Probability Mass Function seperti dijelaskan di atas hanya digunakan untuk variabel discrete atau categorical. Sebagai contoh seperti melempar dadu, kasus ini mengikuti discrete distribution karena tidak ada nilai yang di tengah-tengah (dadu bermata 6 hanya memiliki kemungkinan angka 1,2,3,4,5,6, tidak mungkin kita mendapatkan angka 1.5).
Selain itu, setiap kemungkinan nilai di PMF pasti memiliki nilai lebih dari 0 serta total seluruh kemungkinan yang ada berjumlah 1. Kenapa begitu? semisal kita melakukan pelemparan dadu maka dapat dipastikan kita akan mendapatkan salah satu dari 6 kemungkinan hasil pelemparan dadu (1 hingga 6). Jika dibuat tabel, kemungkinan dari pelemparan dadu tersebut adalah sebagai berikut:
Dengan melihat tabel di atas, total dari seluruh kemungkinan yang ada akan menjadi 1.
Tipe-tipe discrete distribution
Tergantung dari sifat data yang menjadi objek penelitian, tipe distribusi yang bisa digunakan dapat berbeda. Sebagai contoh:
Binomial distribution yaitu salah satu discrete distribution yang memodelkan kemungkinan mendapatkan satu dari dua hasil yang mungkin terjadi (binary), semisal melempar koin.
Poisson distribution memodelkan variasi kemungkinan suatu total kejadian pada suatu rentang waktu. Sebagai contoh Jika kita mengetahui kejadian “Banjir” terjadi, secara rata-rata, “3” kali per “bulan”. Maka dapat kita modelkan variasi kemungkinan terjadinya “banjir” dari rata-rata kejadian yang terjadi dan dapat juga melihat batas minimum ataupun maksimum total kejadian yang dapat terjadi pada suatu rentang waktu.
Uniform Distribution memodelkan kejadian yang memiliki kemungkinan sama untuk seluruh kejadian yang ada. Sebagai contoh adalah kejadian melempar dadu.
Probability Density Function (PDF)
Bila suatu variabel bisa memiliki nilai tak terbatas antara dua nilai maka variabel tersebut dapat mengikuti Probability Density Function (PDF). Sebagai contoh yaitu tinggi badan dan gaji pegawai. Berbeda dengan PMF, kemungkinan suatu nilai di PMF dapat memiliki nilai 0. Sebagai contoh, kemungkinan mengukur tinggi seseorang tepat 175 cm (tidak lebih besar atau lebih kecil berapa pikometer) adalah 0 atau setidaknya mendekati 0.
Kemungkinan pada PDF diukur berdasarkan range nilai, bukan berdasarkan satu nilai saja. Sebagai contoh, semisal kita mempunyai sampel persebaran IQ dari nilai 20 hingga 180 dengan mean sampel 100 dan Standard Deviation 20. Persebaran data tersebut dapat dilihat pada gambar di bawah:

Pada persebaran data diatas, semisal kita ingin mengetahui kemungkinan untuk mendapatkan sampel dengan IQ dibawah 90. Kita dapat menghitung kemungkinan tersebut dengan mengukur total area yang diarsir atau area under the curve. Perhitungan yang dilakukan bisa dilihat pada artikel ini. Pada data di atas, dapat kita lihat bahwa jika kita mengambil data secara acak, kemungkinan kita mendapatkan sampel dengan IQ dibawah 90 adalah sebesar 42.37%
Kesimpulan
Dengan mempelajari Probability Distribution, kita mampu mendapatkan kemungkinan suatu nilai pada saat kita melakukan pengambilan acak. Hal ini penting untuk dipelajari karena konsep probability distribution adalah salah satu inti dari dunia data science.
Pada artikel berikutnya saya akan mencoba membahas berbagai jenis probability distribution serta bagaimana kita menentukan sebenarnya data kita termasuk distribusi yang mana.
See ya!