Traditional Bootstrap and Block Bootstrap. What is the Differences? - NBD Lite #22
The differences in resampling technique.
If you are interested in more audio explanations, you can listen to the article in the AI-Generated Podcast by NotebookLM!👇👇👇
Bootstrap is a resampling technique used to estimate the sampling distribution of a statistic by repeatedly resampling from the data.
The idea is to use the available data to approximate the population by generating multiple samples (with replacement) from the available data to understand the statistical variability.
Bootstrap is even applied in the machine learning model, the ensemble model Bagging, such as Random Forest.
There are Traditional Bootstrap and Block Bootstrap.
What are the differences? That’s what we are going to discuss today!
Here is the summary for you👇
Traditional Bootstrap
As mentioned above, Bootstrap is a statistical estimation method with replacement.
This means the method would resample the original data as the population and draw randomly from that population to generate multiple new datasets.
You can see the illustration of Bootstrap work in the image below.
We have one original dataset, but by resampling the data multiple times with replacement, we end up with N datasets.
So, why are we using Bootstrap?
I have mentioned previously that Bootstrap estimates the sample statistic, such as the mean or median.
Bootstrap is a powerful method that can be used without making assumptions about the underlying data distribution.
It’s a non-parametric method that doesn’t need a normal data distribution, and we can handle a small dataset.
We can also use Bootstrap to develop confidence intervals and perform hypothesis testing where traditional parametric methods are not applicable.
For example, we can perform Bootstrap to estimate the data mean confidence interval with the code below.
import numpy as np
from sklearn.utils import resample
data = [2, 3, 5, 7, 11]
# Number of bootstrap samples
n_iterations = 1000
bootstrap_means = []
# Bootstrap process
for i in range(n_iterations):
bootstrap_sample = resample(data)
bootstrap_means.append(np.mean(bootstrap_sample))
# Confidence Interval (95%)
lower_bound = np.percentile(bootstrap_means, 2.5)
upper_bound = np.percentile(bootstrap_means, 97.5)
print(f"Original Mean: {np.mean(data)}")
print(f"Bootstrap 95% Confidence Interval for the Mean: [{lower_bound}, {upper_bound}]")Original Mean: 5.6
Bootstrap 95% Confidence Interval for the Mean: [3.0, 8.6]
We can see that using Bootstrap, we can assess the estimated interval for the population mean from the sample.
This method above is what we call the Traditional Bootstrap. A few notes about them are:
The data points should be independent and identically distributed.
There is no correlation between the data points.
Resample individual data points where each data point has an equal chance to be resampled.
It’s a robust method, but there are some weaknesses to remember:
Ignores any dependence or autocorrelation in the data.
This can lead to biased estimates if used for dependent data.
With the weakness above, we would use a much more appropriate bootstrapping method called Block Bootstrap.
Block Bootstrap
The Block Bootstrap idea is generally the same as the Traditional Bootstrap.
We resample with replacement from the original dataset to generate multiple datasets to estimate the statistic.
However, there is a difference. Instead of resampling individual data points, we are resampling a data block.
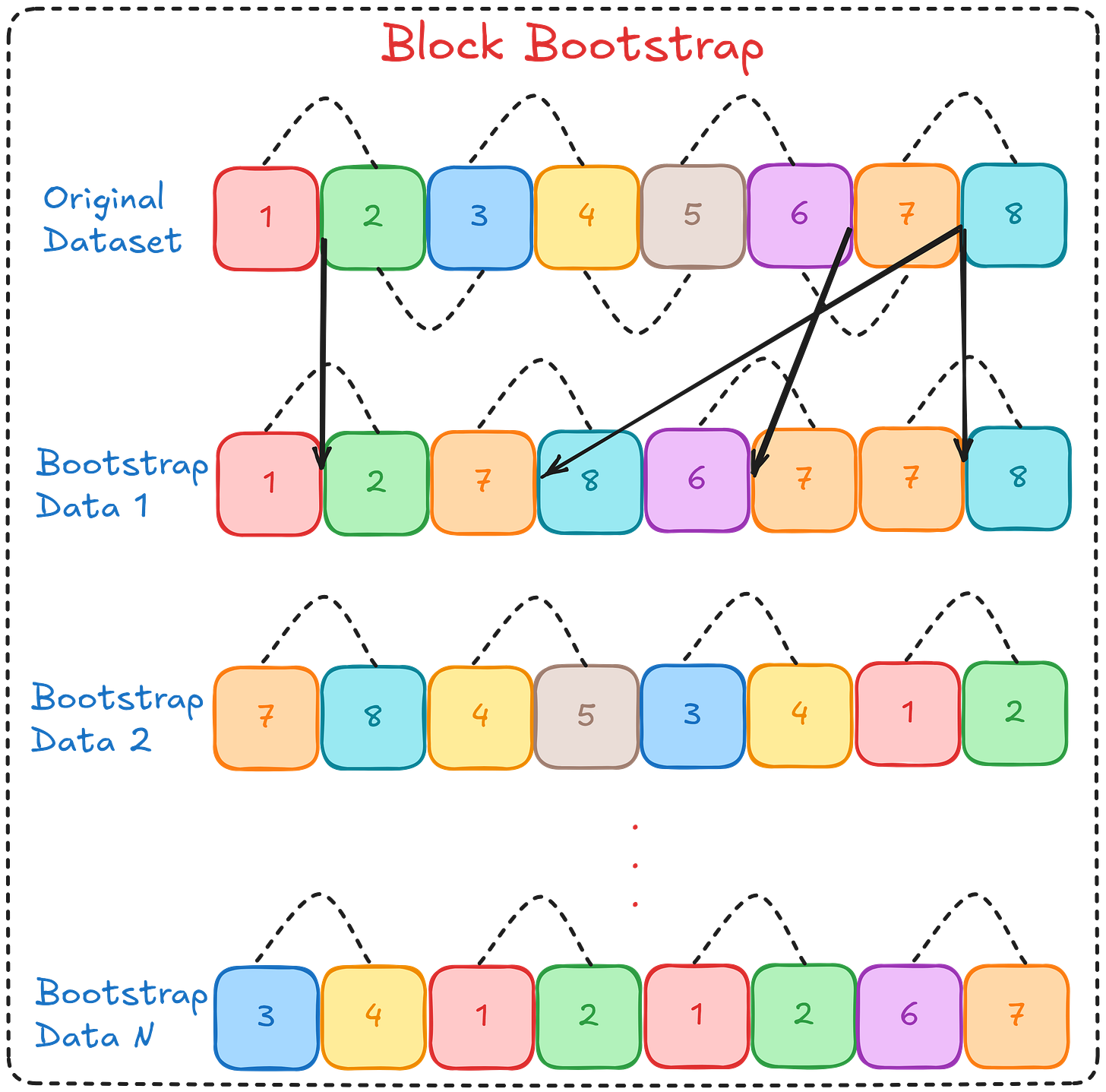
Let’s see the illustration below.
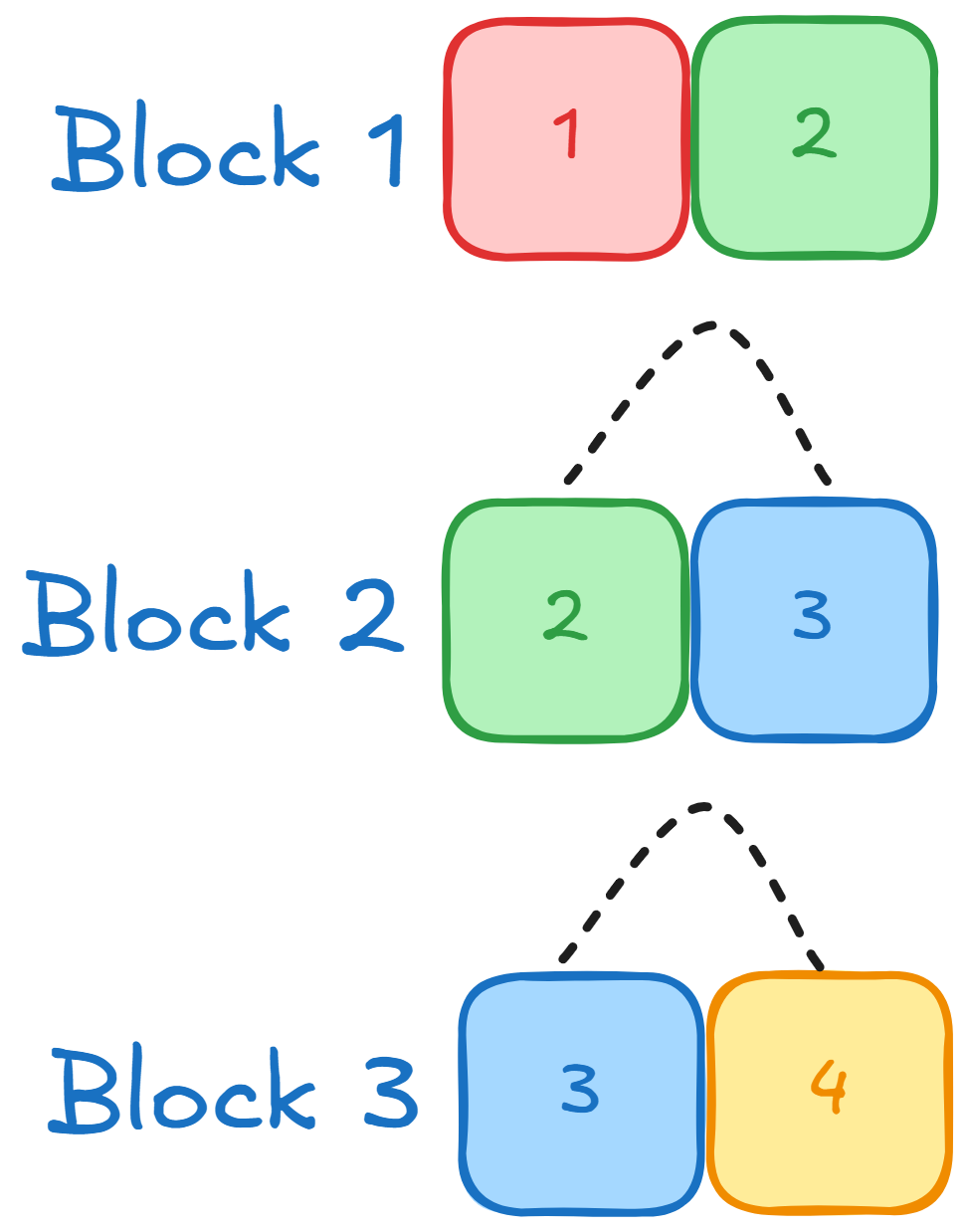
In the illustration above, we resampled consecutive data points (blocks) with two block sizes.
Each block above has two individual data points with two sliding window sizes. For example, one block contains data points (1,2), and another includes data points (2,3).
We resampling the block rather than the individual data points.
So, why are we using the Block Bootstrap? It’s a method designed for dependent data, meaning each data point within the dataset is correlated.
Block Bootstrap is suitable for datasets such as time series or spatial data.
The Traditional Bootstrap can lead to bias as it ignores dependence. So, the Block Bootstrap method retains the correlation structure within blocks to correct bias.
We can implement Python code for Block Bootstrap using the arch package.
from arch.bootstrap import MovingBlockBootstrap
import numpy as np
import pandas as pd
np.random.seed(42)
data = np.random.normal(0, 1, 100)
df = pd.DataFrame({'value': data})
block_size = 10
bootstrap = MovingBlockBootstrap(block_size, df['value'])
n_iterations = 1000
bootstrap_means = []
for data in bootstrap.bootstrap(n_iterations):
sample = data[0][0]
bootstrap_means.append(sample.mean())
bootstrap_means = np.array(bootstrap_means)
print(f"Original mean: {df['value'].mean()}")
print(f"Block Bootstrap mean: {bootstrap_means.mean()}")Original mean: -0.10384651739409384
Block Bootstrap mean: -0.12627284861650548
What is essential about Block Bootstrap is selecting the block size, which determines how well the dependency structure is preserved.
If the block size is too small, it might not be able to capture the actual dependence. However, too big might lead to less variability in the resampled datasets.
There are many methods to choose the block size, for example, n^1/3, where n is the number of data. Formal methods, such as the Lahiri method, find the ideal block size by minimizing the Mean Square Error.
There are a few methods as well on how to select the blocks of data, including:
Moving Block
This is a fixed block size for the block of data method, such as the abovementioned illustration. Every block would have a fixed number of data points.
Stationary Block
The method of selecting the block lengths at random typically would still be close to the chosen mean. Also, the block could start from a random position.
Circular Block
The data is selected similarly to the moving block but is treated as circular or can wrap around. If the block reaches the end of the data, it continues from the beginning.
That’s all the basics you need to know about the differences between Traditional Bootstrap and Block Bootstrap.
Are there any more things you would love to discuss? Let’s talk about it together!
👇👇👇