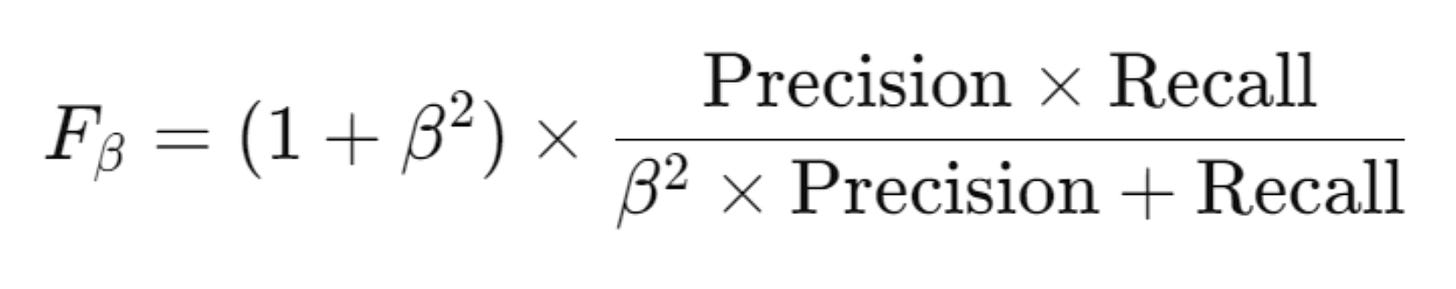Understanding F-Beta For Model Evaluation - NBD Lite #29

Improve the way to evaluate your model classifier.

Model evaluation is a must-do activity when developing the machine learning model.

In the case of the classification model, we have metrics more than accuracy.

There are selections such as Precision, Recall, and F1-Score, depending on where we want to focus.

The F1 score is usually the go-to for balanced precision and recall metrics.

However, do you know that we could tweak the score even further to give some emphasize to either Precision or Recall?

This is where the F-beta score comes into play.

So, how does it work? Let’s get into the detail! Here is the summary.

---

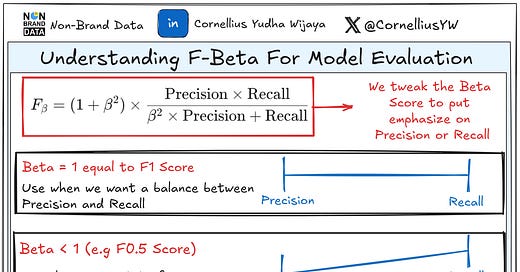
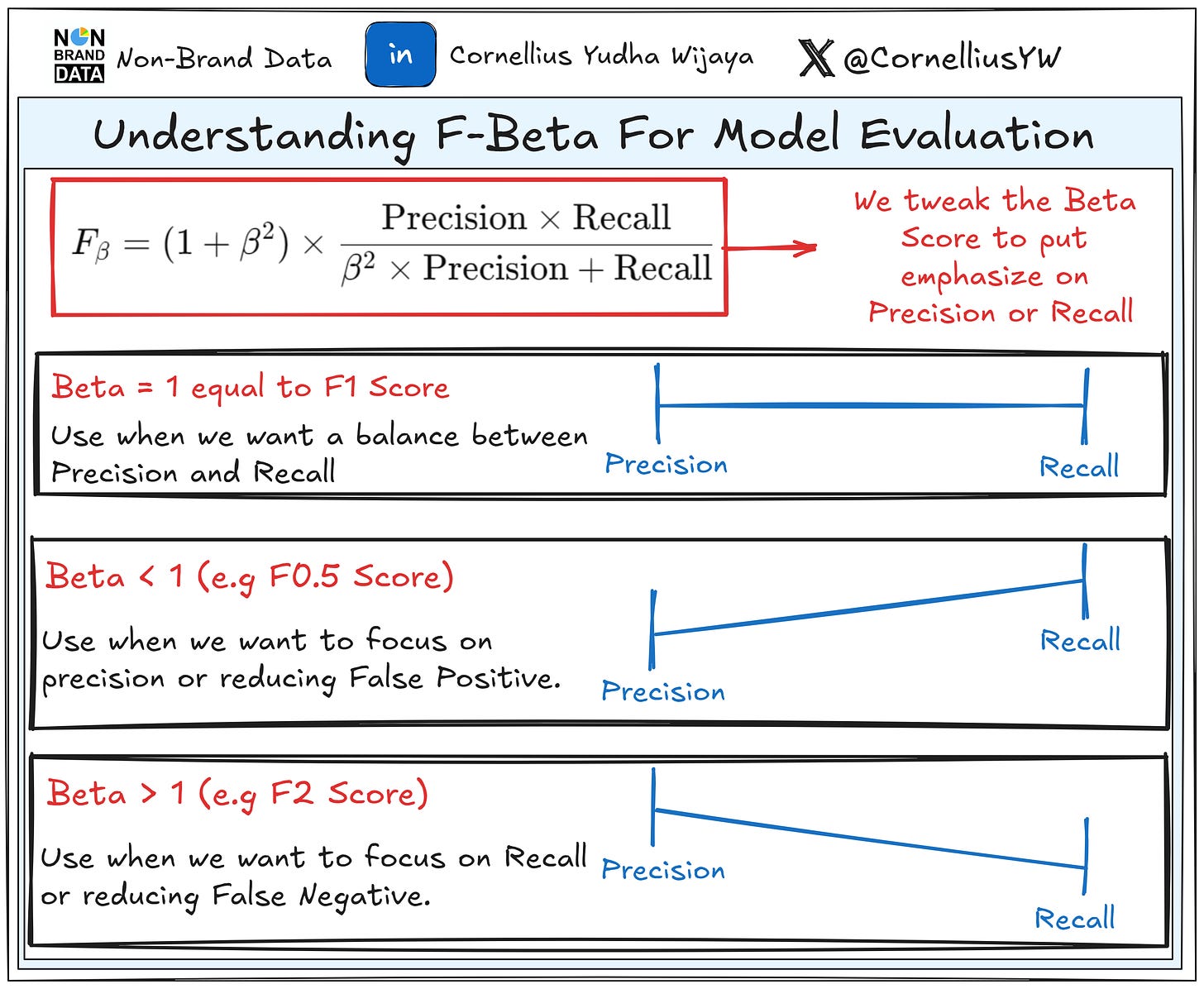
F-Beta Score

The F-beta score is an extension of the F1-Score that allows you to prioritize precision or recall by adjusting the weight of each metric.

It’s become an important metric when we want to have certain degrees of emphasize on either precision or recall but not neglect the other completely.

We can calculate F-Beta Score as:

The parameter β (beta) would adjust the importance of recall or precision.

Generally, this happens when we adjust the β parameter,

• β > 1: More focus on recall. Useful for medical diagnostics (e.g., detecting rare diseases).

• β < 1: More focus on precision. Useful for fraud detection or spam filtering to minimize false positives.

• β = 1: Balances precision and recall, giving you the F1-score.

---

So, why do we want to use the F-Beta Score?

There are many instances in which the F-Beta score is useful, including:

1. Precision and recall are not equally important, but we don’t want to neglect one over the other.

2. Imbalanced datasets require a more versatile evaluation (e.g., fraud detection with few positive cases).

3. Depending on the use case, you want to align model evaluation with business goals, such as focusing on false positives or false negatives.

---

Python Code Example

Let’s try the Python code example to use the F-Beta score.

We can implement them using Scikit-Learn.

from sklearn.metrics import fbeta_score

#Prediction and Ground Truth
y_true = [1, 1, 1, 0, 0, 0, 1, 0, 1, 0]
y_pred = [1, 0, 1, 0, 0, 1, 1, 0, 0, 0]

# Calculate F-beta with beta = 2 (more focus on recall)
f2 = fbeta_score(y_true, y_pred, beta=2)
print(f"F2-Score (Recall Focused): {f2:.2f}")

# Calculate F-beta with beta = 0.5 (more focus on precision)
f05 = fbeta_score(y_true, y_pred, beta=0.5)
print(f"F0.5-Score (Precision Focused): {f05:.2f}")

F2-Score (Recall Focused): 0.62

F0.5-Score (Precision Focused): 0.71

As you can see, the exact prediction and ground truth provide different scores.

The F2-Score means it evaluated with more weight on recall. This means it prioritizes identifying as many true positives as possible, even at the cost of making some false positives.

In contrast, the F0.5-Score means it evaluated with more weight on precision. It prioritizes ensuring that predicted positives are truly positive, even if it means missing some actual positives (lower recall).

Try to play around with the β parameters to align with your needs.

---

That’s all you need to know why the F-Beta score is important.

Are there any more things you would love to discuss? Let’s talk about it together!

👇👇👇

---