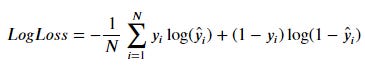Why you should use Log Loss to Evaluate your Model
Understanding the less widely used metrics
In a classification machine learning model, we assign a probability of the label given the features. For example, Label “Yes” is 0.7 or “No” is 0.3. The output is what we want for any machine-learning model.
However, how confident are we with the given probability? The model might have provided probability output 1, meaning the model is 100% confident of the prediction. But are we sure we can trust the model probability output itself?
This is why we want to use a loss function—high values for confident but wrong prediction and low values for correct prediction. In classification machine learning, the typical loss function we could use is Log Loss.
What is Log Loss, and how would it be helpful in your evaluation? Let’s get into it.
Log Loss
Log Loss or Cross-Entropy is a loss function to calculate how close our model prediction probability is to the actual label. The further the predicted probability from the actual value, the higher the log loss value was.
The log Loss equation is stated in the following image:
Where N is the number of examples, y_i is the actual label (0 or 1), and y_hat is the probability prediction of the positive class.
We can extend the equation into the Multi Class label with the following equation.
where M is the number of classes, and y_ij is the actual label for each data i for class j.
Enough about the math equation and why we should use log loss score.
Why Consider Log Loss for Evaluation
There are several reasons why we want to consider using Log Loss for evaluating our machine learning model, including:
Log loss penalty: The log loss would penalize the incorrect predictions severely when the predicted probability is high. A model overconfident in its predictions will produce high log loss score than a model that is more uncertain about its predictions.
Scale-invariant: Log loss was not affected by the scale of the predictions, which is a valuable property when comparing models that might make different scale predictions.
Following a proper scoring rule: Log loss is optimized by the actual class probabilities compared to accuracy, which is only optimized when the predicted class is the same as the actual class.
In summary, log loss is a good measurements if we want to be confident in our model probability prediction.
However, there are a few caveats we need to know when using log loss as a measurement score:
Log loss only measures the performance of a model in probability. If you need an accuracy score, then it might not be suitable.
Log loss is sensitive to class imbalance. Suppose there is a significant imbalance in the distribution of classes; the performance of the majority class may dominate log loss.
Log loss can be computationally expensive for large datasets. As log loss is calculated for each data row, it could be a burden during calculation.
Although with the caveat above, log loss is still an excellent measurement. Let’s see the application of log loss.
Log Loss with Example
We can rely on the scikit-learn package in the data pipeline to calculate the log loss score. To do that, we can use the following code.
from sklearn.metrics import log_loss
#y_true is the actual label and y_pred is the prediction probability
log_loss(y_true, y_pred)With the above code, we would get the log loss score. But how could we assess that our log loss score is already low enough? Lower is better, but how low?
In the application, we would run the above equation to acquire the score for each prediction, similar to the table below.
The higher the log loss score was, the bad the prediction was. To get the overall sense of the model, we would need to get the log loss average score.
If we take an average of the score above, we will achieve an average score of 0.969. So, is this score good or bad?
In a sense, the further the score from 0, it’s a bad one. However, it would be more intuitive if we had a baseline log loss to compare with. In ideal circumstances, we want our log loss score to be better than the random prediction's log loss. So, we need to have the baseline score for the random model.
Let’s use Python code to calculate that. I would adopt the code that came from Nishant Mohan.
Our example above has five observations with a 2:3 data ratio. If we implement them into the code:
from sklearn.metrics import log_loss
def calculate_log_loss(class_ratio,multi=10000):
if sum(class_ratio)!=1.0:
print("warning: Sum of ratios should be 1 for best results")
class_ratio[-1]+=1-sum(class_ratio) # add the residual to last class's ratio
actuals=[]
for i,val in enumerate(class_ratio):
actuals=actuals+[i for x in range(int(val*multi))]
preds=[]
for i in range(multi):
preds+=[class_ratio]
return (log_loss(actuals, preds))
print('Baseline Log Loss: ', calculate_log_loss([.4, .6], 5))The Baseline result Log Loss score is 0.673. Since we want our score to be better (lower) than the baseline, our result above is not good. This means we need to make some adjustments to our data and model.
Conclusion
Log Loss is an evaluation score used to assess whether our model probability prediction can be trusted. As log loss is a loss function, the lower the score, the better our model predictions are.